데카르트가 남긴 업적은 다양하지만, 발상의 전환으로 남긴 업적은 좌표와 그에 기반한 함수의 개념이다. 모든 공간을 좌표상에 배열할 수 있다는 아이디어는 이후 다차원계와 시공간 인식에 대한 연구의 시초가 되었다.
좌표축과 함께 시공간에 대한 인식을 바꾼 연구는 행렬과 행렬역학이다. 그 유명한 Cleve Moler가 행렬을 표현한 말이다.
Matrix - The mother of all data structures. The non-mathematical uses of the word 'matrix' reflect its Latin origins in 'mater,' or mother... The word has two meanings - a representation of a linear mapping and the basis for all our existence.
좌표축을 정의하는 방법은 다양할 수 있다. 많은 사람에게 익숙한 직교 좌표계나 구면좌표게 등도 있지만 조금만 찾아보면 coordinate(좌표축)를 정의하는 엄청나게 많은 방법을 찾을 수 있다. 아무리 복잡하다고 하지만 그래도 분야마다 일종의 스탠다드가 존재한다. 물리학과 컴퓨터 공학 양쪽을 다루기 때문에 좌표계를 다루는 부분의 차이로 가끔 고생할 때가 있다. 본질로 들어가면, 초등학교때 잠시 다녔던 컴퓨터 학원에서부터 그 혼란이 시작되었겠다.
베이직에서 화면에 글씨의 위치를 정해서 출력하기 위한 명령으로, 커서의 위치를 지정하는 LOCATE라는 명령이 있다. 커서를 옮기려면
30 LOCATE(3,45)
식이다. 3행 45열의 좌표에 커서를 가져다 놓으라는 설명이다. 굉장히 행렬스러운 표현이며, 물리학자들에게는 별 어려움없이 받아들여질 표현이다. 그런데 화면에 UI를 그릴때를 생각해보자. 토이 라이브러리의 경우
Canvas canvas(450, 450, "Recostruct map"); canvas.SetDomain(25, 25, 400, 400); canvas.SetForeground("blue");
식이다. 좌표를 정의할 때의 순서는 (가로 위치, 세로 위치) 의 set을 사용하게 된다. 따라서 여기서의 값은 일반적인 2차원 좌표계에서의 (x,y) 값에 해당된다. 웹페이지에서 각 구성 요소들의 위치를 지정하거나 크기를 지정하는 CSS 문법이나, 가상 3차원 좌표계에서 객체를 생성하는 Direct3D의 기본 명령들도 2차원 투영의 기준은 (x,y)가 된다. 행렬을 기준으로 화면에 대응을 시키는 경우, 일반적인 2차원 좌표계에 대응시키면 축은 (y,x)가 기준이 되니, 두 축을 기술하는 순서가 바뀌는 셈이다.
석사 입학때 면접을 보는 자리였다. 역학 면접이었는데, 문제를 주면 칠판에 바로 문제를 풀면서 기술하는 내용에 대하여 설명을 하는 식이었다. 역학은 어려움을 느끼지 않았기에 (역설적이게도 당시 가장 싫어하던 분야가 통계 물리학이었다 -_-) 칠판에 주욱 써내려가며 어려움없이 답을 냈다.
앞에서 전개를 보던 교수분들이 중간 과정을 따라오면서는 아무 말이 없다가, 결과를 보더니 전부 고개를 갸웃거렸다. '틀렸나?' 싶어서 다시 전개를 머릿속에서 해 보았는데, 중간에 계산이 복잡하기는 했지만 틀린 부분은 없어 보였다. 꽤 긴 적막을 깨고서 교수 한 분이 말을 꺼냈다. "답이 틀렸는데 크기는 맞고, 계산을 따라가 보았는데 틀린 곳은 없고..."
그러더니 한 분이 갑자기 질문을 했다. "한 번 칠판에 3차원 cartesian coordinate(직교 좌표계)를 그려봐요." 그렸다. 그러니 면접 자리의 긴장이 풀렸다. "좌표축의 방향이 일반적인 방향과 반대가 되어있군." 이후에는 평범한 이야기. 보통 좌표축을 그 방향으로는 쓰지 않는다는 이야기라거나, 결과에서 끌어낼 수 있는 생각등이 어떤 것이 있는지에 대한 질문들이었다.
당시에 취미 비슷하게 X11을 이용한 그래픽 출력 프로그램을 하나 만들고 있었다. 화면을 다룰때의 굉장히 일반적인 형태로 좌표축을 잡아 만들고 있었다. 가로로 x축, 세로로 y축, 화면의 심도를 z축으로 잡는다. x축과 y축을 정의하고, 깊이를 화면 밖으로 나올 수록 양의 값으로 잡았다. 그리고 개체를 그릴 때 어떤 값이든 그 좌표계의 x축과 y축에 맞게 투영해서 만들었다.
그게 좌표축에 혼동을 가져왔던 것이었다.
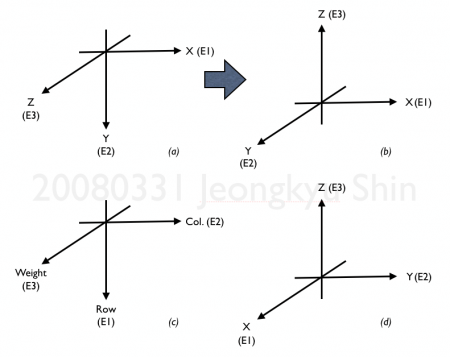
a)는 일반적으로 화면을 다룰 때의 좌표, b)는 이를 회전시킨 같은 좌표이다. c)는 행렬을 기반으로 한 좌표이고 d)는 물리학에서 일반적으로 쓰는 직교좌표계이다. E1, E2, E3는 좌표를 set 형태로 나타낼때의 순서이다. (E1, E2, E3). b)와 d)는 달라보이지만, b)를 z축 중심으로 시계방향으로 돌리면 y축의 방향이 반대로 되었을 뿐이다.
아무리 시간이 지나도 혼동이 줄어들지 않는다. 처음 베이직에서 LOCATE와 POINT 명령의 차이로부터의 혼동이 15년이 넘는 시간동안 끊임없이 따라온다니 대단하다. 가끔 심심하면 머릿속에서 두 좌표축을 가지고 혼자 연습을 한다.
단지 거울상일 뿐인데, E2를 기술하는 방향의 부호가 정반대일뿐인데 그걸로 상상해 볼 수 있는 것들이 정말 많이 바뀐다. 다른 모든 것이 동일하다고 해도 축 하나의 차이가 엄청나게 많은 변화를 가져오는 수많은 것들을 본다. 단백질 구조에서, 식물 성장의 위상 속에서, 그리고 매일 살아가는 사회 속에서도.
좌표축중에 단지 하나만 바뀌었을 뿐인데.