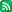굉장히 어렵게 보이지만 RG의 기본은 결국 스케일이 없는 경우 재규격화를 통해서 본래 시스템의 '도구'들을 그대로 가지고 가서 사용할 수 있다는 부분에 있다. 그리고 그걸 이해하는 동시에 RG가 얼마나 일반화하기 어려운가 알게 된다. RG를 이해하게 되면 거꾸로 프랙탈 구조가 왜 자연계에 존재하는지에 대한 통찰의 조각을 얻을 수 있다. 비선형 동역학과 복잡계를 공부하다보면 가끔 그렇게 통찰의 조각을 줍는 포인트가 있다. 포인트의 위치는 사람마다 다르겠지만. (연구참여생들에게 설명하다가 그 위치가 다름을 문득 알게 되었다.)
*
통계역학, 비선형 동역학, 복잡계의 수많은 개념들은 양자역학만큼이나 다른 분야에서 메타포로 많이 활용된다. 그렇지만 RG만큼은 그 중요성에 비해서 인문학쪽에서 널리 메타포로 활용되고 있지 않다. 개인적인 생각으로는 좀 놀라운 일이다. 스위프트의 그 유명한 그림이 아니더라도 RG는 정말 메타포로 이용해 먹기 좋다.
RG가 메타포로의 응용 정도가 떨어지는 이유는 이해가 어렵다는 부분에 있지 않나 싶다. 다른 분야들에서 메타포로 원용되는 물리학의 개념들은 공통점이 하나 있다. (그게 맞든 틀리든) 의미하는 바를 한 문장으로 요약이 가능하다는 점이다. 그런데 불행히도 RG는 그게 좀 힘들다. 굳이 하라면 못할것도 없겠지만, "크기에 상관없이 항상 비슷하게 보이는 시스템"의 메타포는 프랙탈이 벌써 가져가버렸다. - 게다가 프랙탈 그림은 예쁘기도 하거니와 해안선 설명은 이해도 쉬워보인다.

프랙탈은 그림만 봐도 뭘 의미하는 지 알 수 있다. 그러니 메타포로 써먹히기는 훨씬 좋다.
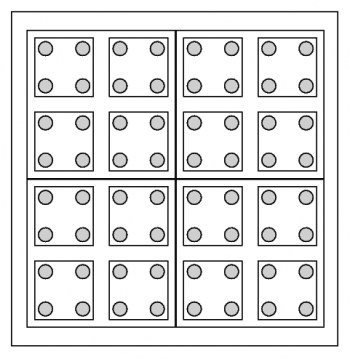
Renormalization group을 도식적으로 나타낸 L. P. Kadanoff 의 유명한 그림.
'요원'이 되기 위해서 한국사를 공부하며 그 안에서 재규격화 과정으로 설명할 수 있을것만 같은 부분을 여럿 보았다. 스케일에 따라서 달라보이지만 같은 식으로 표현할 수 있을것만 같은 고대 생활사와 국가 흥망사들은 잡상하기에 참 좋은 주제이다. 그리고 당연히 복잡한 변화가 있는 시스템이라 critical temperature 주위에 위치한 시스템일테고, 그러한 특성이 만들어내는 결과가 혼돈처럼 보이는 변화들과 함께 모두 예측 가능하다는 시사점이 씁쓸하게 한다. 다행이라면, 아직까지 연대표 분석을 통한 RG에 대해 측정한 시도가 없다는 점 덕분에 이러한 잡상이 잡상으로 끝난다는 점이다. (사람의 수명이 대충 45세 정도이기 때문에 해상도와 데이터 포인트 수에 문제가 있다)
어째서 시대는 계속 발전하지만 사람은 항상 그대로일까. 과거로부터의 교훈은 기록으로 남는데 어째서 그러한 교훈들은 책 속에만 이렇게 굳어있게 되는 것일까. 생각은 깊어지고 머리는 아파지는 주제이다.