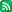$$ F = \frac{d^2 r}{dt^2} $$ $$ \Rightarrow F_i (r_i (t),t) = \frac{d^2r_i}{dt^2} $$
$$ \simeq \frac{r_i(t+h) + r_i(t-h) -2r_i(t)}{h^2} $$
$$ \Rightarrow r_i(t+h) \simeq 2r_i(t) - r_i (t-h) + h^2F_i(t) + O(h^4) $$
$$ r(-h) = r(0) - hv(0) + \frac{h^2}{2} F(0) $$ ( $$v(0)$$ = 초기속도 )
$$ r(0), r(-h) $$ 에서 $$r(h)$$ 구할 수 있다.
$$ \Rightarrow v_i(t) \simeq \frac{r_i(t+h)-r_i(t-h)}{2h} + O(h^2) $$
이의 과정을 반복하여 업데이트한다.
알고리즘에서 알 수 있듯 Euler method와 같은 이유로 오차가 발생할 수 있지만, 이 경우는 dynamics의 추적이 아니라 equilibrium condition으로의 수렴이므로 오랜 iteration 이후에는 동일한 결과를 얻게 된다.
Mind Forest: Beneath imaginations - 시간의 토양에 기억의 나무를 심으며

시간의 토양에 기억의 나무를 심으며 - inureyes
분류 »
Mind Forest: Beneath imaginations - 최근 트랙백
요새 달린 트랙백들 »
-
2020 / google rankinggoogle ranking
-
2020 / google rankinggoogle ranking
-
2020 / right nowright now
-
2020 / this profilethis profile
-
2020 / PokerPoker
Mind Forest: Beneath imaginations - 최근 댓글
요새 달린 댓글들 »
-
2014 / lunamoth차세대 출판 부분은 텍스트...
-
2013 / inureyes오래간만이야! 요샌 어떻게 ...
-
2013 / 비밀방문자관리자만 볼 수 있는 댓글입...
-
2012 / inureyes혹시 본문 중 어딘가 태그가...
-
2012 / 이재영안녕하세요. 불쑥 글을 남...
37 명이 RSS를 구독하고 있습니다.
Counter
- Total
- 2113320
- Today
- 275
- Yesterday
- 472